CoordinatesPupils should be taught to:. describe positions on a 2-D grid as coordinates in the first quadrant.
describe movements between positions as translations of a given unit to the left/rightand up/down. plot specified points and draw sides to complete a given polygon.Notes and guidance (non-statutory)Pupils draw a pair of axes in one quadrant, with equal scales and integer labels. Notes and guidance (non-statutory)Pupils become accurate in drawing lines with a ruler to the nearest millimetre, and measuring with a protractor. They use conventional markings for parallel lines and right angles.Pupils use the term diagonal and make conjectures about the angles formed between sides, and between diagonals and parallel sides, and other properties of quadrilaterals, for example using dynamic geometry ICT tools.Pupils use angle sum facts and other properties to make deductions about missing angles and relate these to missing number problems. Geometry – position and directionPupils should be taught to:.
Coordinate Grid Games Dino Dig 2
identify, describe and represent the position of a shape following a reflection or translation, using the appropriate language, and know that the shape has not changed. Notes and guidance (non-statutory)Pupils recognise and use reflection and translation in a variety of diagrams, including continuing to use a 2-D grid and coordinates in the first quadrant. Notes and guidance (non-statutory)Pupils draw shapes and nets accurately, using measuring tools and conventional markings and labels for lines and angles.Pupils describe the properties of shapes and explain how unknown angles and lengths can be derived from known measurements.These relationships might be expressed algebraically for example, d = 2 × r; a = 180 − (b + c).
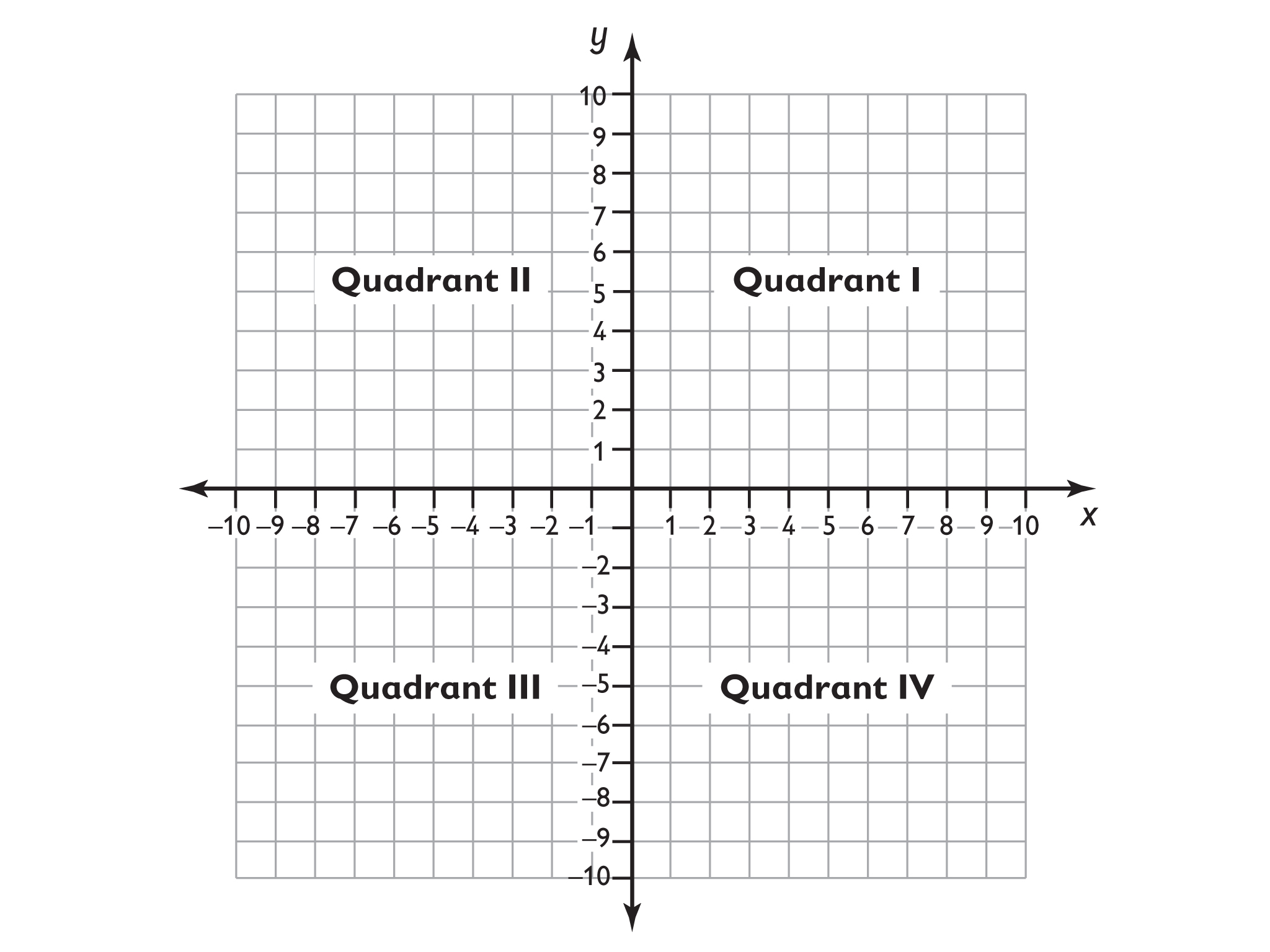
Geometry – position and directionPupils should be taught to:. describe positions on the full coordinate grid (all 4 quadrants). draw and translate simple shapes on the coordinate plane, and reflect them in the axes. Notes and guidance (non-statutory)Pupils draw and label a pair of axes in all 4 quadrants with equal scaling. This extends their knowledge of one quadrant to all 4 quadrants, including the use of negative numbers.Pupils draw and label rectangles (including squares), parallelograms and rhombuses, specified by coordinates in the four quadrants, predicting missing coordinates using the properties of shapes. These might be expressed algebraically for example, translating vertex (a, b) to (a − 2, b + 3); (a, b) and (a + d, b + d) being opposite vertices of a square of side d.